What is the correct position and rotation?

Position

If you want to place mesh to have it's center-of-gravity at the origin that is indeed fairly simple (center of gravity is simply calculated by summing all vertices and dividing the resulting value by the number of vertices), i.e.:

float4 centerOfGravity = float4(0.0f, 0.0f, 0.0f, 0.0f);
for (int i = 0; i < mesh.vertices.size(); i++)
{
    centerOfGravity += mesh.vertices[i];
}
centerOfGravity /= (float)mesh.vertices.size();

You simply translate all vertices by -centerOfGravity (or create transformation matrix for the object with translation -centerOfGravity).

There are of course alternatives (like computing AABB - get centroid of it and use that instead of center of gravity).

Rotation

Now this one is problematic - it depends on - how do you want to rotate your geometry on default? Is it already correctly rotated when exported from 3D editor, or generated? Or do want to find minimal bounding box and rotate in a way, that longest axis is F.e. your Y axis?

Minimal OBB can be found like following

1. Calculate the centroid (c0, c1, c2) and the normalized covariance
2. Calculate the eigenvectors e0, e1, e2. The reference system basis will be (e0, e1, cross(e0, e1))
3. Transform the points into that reference system. Transformation will be given by rotation matrix (e0, e1, cross(e0, e1)) and translation centroid (c0, c1, c2), resulting 4x4 matrix has to be inverted to be used.
4. Calculate min, max and center diagonal
5. Now, the transformation you have to apply is rotation (e0, e1, cross(e0, e1)) and translation is rotation * center diagonal + centroid (c0, c1, c2)

Note: cross denotes a vector product

If you want more deeper description/understanding of this - look up OBB generation with Principal Component Analysis. Also a bit of knowledge on linear algebra is needed (at least what are eigen vectors and eigen numbers, etc.). With the above you will be able to transform your geometrical model in a way that the model's longest axis is pointing along let's say Y axis, but is that the rotation you're seeking?

Note: As of me - I don't rotate models at all, the moment you import them into my engine, drag them into scene - I place them in a way they were exported from the 3D modelling software. User can then rotate them in any way he wants (with rotation tool).

@JoeJ I can give you a bit of details here (it is “almost worthy of an article”. Copied implementation into Unity just to confirm it is correct. Unlike stating to “use eigen” (insert any other linear algebra library - see note), which I wouldn't consider as a proper answer - as I heavily prefer to at least implement it myself to understand what is actually going on underneath.

Note: I still mostly use my own linear algebra libraries in my projects, which are comparable in speed with large templated libraries (I use SIMD after all) - while I do have used them and recognize them for them being generic and generally quite usable, in my projects I prefer to not use them (mainly to keep source code readable).

Now, time for the description:

How to build Oriented Bounding Boxes

How is it calculated (in pseudo code):

Generate()
{
    CalculateCovarianceMatrix();
    GenerateEigenVectorBasis();
    CalculateCentroidAndBounds();
}

Covariance Matrix

The matrix we need to calculate from our vertices is basically this:

Per definition we also know that:

So, in short it can be written as:

Keep in mind that definitions for variance and covariance are:

So, in implementation it will be something like:

private Vector3 Mean(Vector3[] data)
{
    Vector3 result = new Vector3(0.0f, 0.0f, 0.0f);

    for (int i = 0; i < data.Length; i++)
    {
        result += new Vector3(data.x, data.y, data.z);
    }

    if (data.Length > 0)
    {
        result /= (float)data.Length;
    }

    return result;
}
    
private Matrix3x3 CovarianceMatrix(Vector3[] data, Vector3 mean)
{
    Matrix3x3 m = new Matrix3x3(0.0f, 0.0f, 0.0f, 0.0f, 0.0f, 0.0f, 0.0f, 0.0f, 0.0f);

    for (int i = 0; i < data.Length; i++)
    {
        m.m00 += (data[i].x - mean.x) * (data[i].x - mean.x);
        m.m01 += (data[i].x - mean.x) * (data[i].y - mean.y);
        m.m02 += (data[i].x - mean.x) * (data[i].z - mean.z);

        m.m10 += (data[i].y - mean.y) * (data[i].x - mean.x);
        m.m11 += (data[i].y - mean.y) * (data[i].y - mean.y);
        m.m12 += (data[i].y - mean.y) * (data[i].z - mean.z);

        m.m20 += (data[i].z - mean.z) * (data[i].x - mean.x);
        m.m21 += (data[i].z - mean.z) * (data[i].y - mean.y);
        m.m22 += (data[i].z - mean.z) * (data[i].z - mean.z);
    }

    float invN = 1.0f / (float)data.Length;

    m.m00 *= invN;
    m.m01 *= invN;
    m.m02 *= invN;

    m.m10 *= invN;
    m.m11 *= invN;
    m.m12 *= invN;

    m.m20 *= invN;
    m.m21 *= invN;
    m.m22 *= invN;

    return m;
}

Eigen Vectors

Eigen vector (Characteristic vector) of linear transformation is a nonzero vector that changes by a scalar factor when that linear transformation is applied to it. Formal definition of calculation is:

Where:

• T is linear transformation
• v is eigen vector
• λ is eigen value associated with v
• I is identity

Now, clearly mathematical way end up in polynomial equation (2nd order polynomial in 2D space or 3rd order polynomial in 3D space). As we're operating in 3D space, there “is” analytical way to solve this (Cardano's solution - based on Tartaglia if I remember correctly) - although it isn't generally used that much as it is quite complex approach. This problem is mostly solved numerically.

Standard way to calculate eigen systems from symmetric matrices is QR decomposition. There is also a slick implementation(which I used) by building orthogonal transform out of rotations representing them by quaternion. The implementation is as following (the number of iterations is a bit overshot … also termination conditions could be “X > 0.99 && X < 1.01” instead of "X == 1" … but you get the idea):

public Quaternion Diagonalization()
{
    int DIAGONALIZATION_ITERATIONS = 24;

    Quaternion q = new Quaternion(0.0f, 0.0f, 0.0f, 1.0f);

    for (int i = 0; i < DIAGONALIZATION_ITERATIONS; i++)
    {
        // v * Q == q * v * conj(q)
        Matrix3x3 Q = new Matrix3x3(Matrix4x4.Rotate(q));

        // A = transpose(Q) * D * Q
        Matrix3x3 D = Q * this * Matrix3x3.Transpose(Q);

        // Non diagonal elements
        Vector3 offdiag = new Vector3(D.m12, D.m02, D.m01);

        // Magnitude of each off diagonal element
        Vector3 om = new Vector3(Mathf.Abs(offdiag.x), Mathf.Abs(offdiag.y), Mathf.Abs(offdiag.z));

        // Find largest off-diagonal value
        int k = (om.x > om.y && om.x > om.z) ? 0 : (om.y > om.z) ? 1 : 2;
        int k1 = (k + 1) % 3;
        int k2 = (k + 2) % 3;

        // Already diagonal - exit iterative computation
        if (offdiag[k] == 0.0f)
        {
            break;
        }

        float theta = (D.GetElement(k2, k2) - D.GetElement(k1, k1)) / (2.0f * offdiag[k]);

        // Make theta positive
        float sgn = (theta > 0.0f) ? 1.0f : -1.0f;
        theta *= sgn;

        float t = sgn / (theta + ((theta < 0.000001f) ? Mathf.Sqrt(theta * theta + 1.0f) : theta));
        float c = 1.0f / Mathf.Sqrt(t * t + 1.0f);

        // Cannot get better anymore
        if (c == 1.0f)
        {
            break;
        }

        // Jacobi rotation for this iteration
        Quaternion jr = new Quaternion(0.0f, 0.0f, 0.0f, 0.0f);

        // Half angle identity - sin(a / 2) = sqrt((1 - cos(a)) / 2)
        jr[k] = sgn * Mathf.Sqrt((1.0f - c) / 2.0f);

        // As our quat-to-matrix convention was v * M, instead of M * v
        jr[k] *= -1.0f;
        jr.w = Mathf.Sqrt(1.0f - jr[k] * jr[k]);

        // Reached limit of floating point precision - terminate
        if (jr.w == 1.0f)
        {
            break;
        }

        q = q * jr;
        q.Normalize();
    }

    return q;
}

Now, the resulting quaternion of this diagonalization is representing spatial rotation into the space of eigen vectors for given matrices. To build up eigen vectors basis you can literally do:

public bool EigenVectors(out Vector3 x, out Vector3 y, out Vector3 z)
{
    Quaternion q = Diagonalization();
    Matrix3x3 m = new Matrix3x3(Matrix4x4.Rotate(q));

    x = new Vector3(m00, m10, m20);
    y = new Vector3(m01, m11, m21);
    z = new Vector3(m02, m12, m22);

    float xMag = Vector3.Magnitude(x);
    float yMag = Vector3.Magnitude(y);
    float zMag = Vector3.Magnitude(z);

    // Here we can handle special cases
    if (xMag > 0.0001f && yMag > 0.0001f && zMag > 0.0001f)
    {
        // All vectors exist
 and have some length
    }
    else if (xMag < 0.0001f && yMag > 0.0001f && zMag > 0.0001f)
    {
	    // When one vector is 0, calculate last one as cross product of the other 2
        x = Vector3.Cross(y, z);

    }
    else if (xMag > 0.0001f && yMag < 0.0001f && zMag > 0.0001f)
    {
	    // When one vector is 0, calculate last one as cross product of the other 2
        y = Vector3.Cross(x, z);
    }
    else if (xMag > 0.0001f && yMag > 0.0001f && zMag < 0.0001f)
    {
	    // When one vector is 0, calculate last one as cross product of the other 2
        z = Vector3.Cross(x, y);
    }
    else
    {
        // When 2 or more vectors are 0, use identity basis (there are better solutions, but I didn't want to dig into details too much)
        x = new Vector3(1.0f, 0.0f, 0.0f);
        y = new Vector3(0.0f, 1.0f, 0.0f);
        z = new Vector3(0.0f, 0.0f, 1.0f);
    }
    
    // To handle issues with numerical precision, iteratively orthonormalize
    for (int i = 0; i < ORTHONORMALIZATION_ITERATIONS; i++)
    {
        Vector3.OrthoNormalize(ref x, ref y, ref z);


        // Check whether we are orthogonal - if so, break the loop
        float dp = Mathf.Abs(Vector3.Dot(x, y) + Vector3.Dot(x, z) + Vector3.Dot(y, z));
        if (dp < 0.001f)
        {
            break;
        }
    }

    return true;
}

This code could be further improved by handling cases where 2 or more vectors are equal (just adding few branches into special cases) to make it proper, full featured solution.

Once we have this basis, it is technically quite straightforward:

Calculate Centroid and Bounds

This is as straightforward as it can get:

Vector3 centroid = new Vector3();

Vector3 min = new Vector3();

Vector3 max = new Vector3();

for (int i = 0; i < vertices.Length; i++)
{
    Vector3 projected = new Vector3();
    projected.x = Vector3.Dot(vertices[i], eigen_basis[0]);
    projected.y = Vector3.Dot(vertices[i], eigen_basis[1]);
    projected.z = Vector3.Dot(vertices[i], eigen_basis[2]);

    if (i == 0)
    {
        min.x = projected.x;
        min.y = projected.y;
        min.z = projected.z;

        max.x = projected.x;
        max.y = projected.y;
        max.z = projected.z;
    }
    else
    {
        min.x = Mathf.Min(min.x, projected.x);
        max.x = Mathf.Max(max.x, projected.x);

        min.y = Mathf.Min(min.y, projected.y);
        max.y = Mathf.Max(max.y, projected.y);

        min.z = Mathf.Min(min.z, projected.z);
        max.z = Mathf.Max(max.z, projected.z);
    }

    centroid += projected;
}

centroid /= (float)vertices.Length;

Results

The result looks like (I drew basis and oriented bounding boxes):

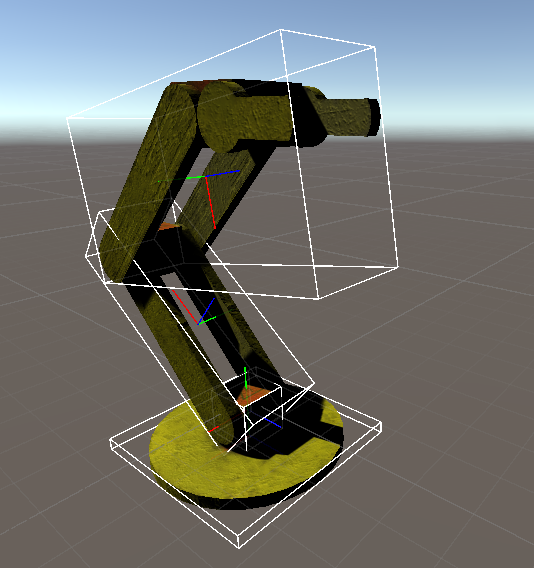
Now, the problem I have with OBBs is that they don't seem that useful (yes, definitely for physics, but in computer graphics we generally prefer to use AABBs). There might be some exceptions like:

• Bounding Volume Hierarchies - in case on uses Multi-Level BVHs, the bottom level could originate from OBB (as it would just update transformation matrix for Top-level BVHs). This could yield some performance gain in most cases - I have never studied it as I never considered this to be worth in the end (if I was a teacher I'd say this might be interesting thesis topic). The performance hit would be negligible (as you have to calculate OBB only once per geometry (or re-build for deformed one)).

So yes, they do have their place, as well as this-like code has place in my linear algebra library for my projects.